Nemendaverkefni

Bls. 39 - Nemendaverkefni 1

Í rammagrein á bls. 39 voru kynnt talnakerfi sem byggja á sætisröð.  Í talnakerfi með grunntölu b (b er jákvæð heil tala stærri en 1) eru notuð b tákn (þ.e.a.s. 0, 1,  ... b-1) og í því er hægt að rita sérhverja tölu á forminu a_nbⁿ + a_n-1b^n-1 + . . . + a₁b¹ + a₀.   Hér standa bókstafirnir a_n ... a₀ fyrir einhverjar talnanna 0, 1, ... b-1 og n er ekki neikvæð heil tala.  Í b-kerfi er tala gjarnan rituð þannig:  (a_na_n-1...a₀)_b.   Þó er venja að sleppa sviganum þegar um tugakerfið er að ræða eða ef af samhengi er ljóst um hvaða talnakerfi er verið að ræða.  Þannig merkir 4261 sama og (4261)₁₀, þ.e.a.s. 4261 = 4·10³ + 2·10² + 6·10¹ + 1·10⁰, en (4261)₈ merkir hins vegar töluna 4·8³ + 2·8² + 6·8¹ + 1·8⁰ sem er jú jöfn tölunni 2048 + 128 + 48 + 1 = 2225 í tugakerfi.

Nú skulum nánar að því hvernig við breytum tölu úr einu talnakerfi í annað.

Svo sem dæmið hér að framan sýnir er auðvelt að breyta úr einhverju b-kerfi í tugakerfi (reiknum einfaldlega út hver talan er skv. skilgreiningu á sætisrithættinum líkt og gert var varðandi töluna (4261)₈).  En hvernig breytum við tölunni 4261 úr tugakerfi í 8-kerfi?

Takið fyrst eftir því að síðasti stafur tölunna 4261 er afgangurinn (leifin) þegar deilt er í hana með 10.  Kvótinn við þá deilingu verður 426.  Með því að deila á ný með 10 í kvótann fæst talan 6 sem afgangur.  Aðrir tölustafir fást síðan (sem afgangar) með endurtekinni deilingu í kvótana.  Ef umbreyta á tölunni 4261 yfir í 8-kerfi er farið eins að nema að nú er deilt með 8.   Þannig fæst

4261 = 8·532 + 5
832 = 8·66 + 4
66 = 8·8 + 2
8 = 8·1 + 0
1 = 8·0 + 1

Í 8-kerfi er því talan 4261 rituð (10245)₈. 

Ef breyta á tölu úr 5-kerfi í 9-kerfi er auðvelt að breyta tölunni fyrst úr 5-kerfi í tugakerfi og síðan úr tugakerfi í 9-kerfi skv. lýsingunni hér að ofan.

Verkefni:  a) Breytið tölunni (47154)₈ í tugakerfi.
                  b) Breytið tölunni (39A7C)₁₄ í tugakerfi.
                  c) Breytið tölunni 47154 í 8-kerfi.
                  d) Breytið tölunni (39A7C)₁₄ í 8-kerfi. 
                  e) Breytið tölunni 689 í 2-kerfi (tvíundarkerfi).
                  f) Breytið tölunni (101110110111)₂ í tugakerfi.
                  g) Breytið tölunni (101110110111)₂ í 16-kerfi (hexadesimalkerfi).

Takið eftir því að (1111)₂ = 15 = (F)₁₆.    Sérhvert tákn í 16-kerfi má því rita sem safn 4 tákna í 2-kerfi (frá 0000 til 1111).  Á líkan hátt má rita tölu sem táknuð er með 8 táknum í 2-kerfi sem tvö tákn í 16-kerfi.  Þannig er (11100101)₂ = (E5)₁₆ því (1110)₂ = (E)₁₆ og (0101)₂ = (5)₁₆.

Verkefni:  a) Breytið tölunni (110 1001 0001 0000)₂ í 16 kerfi og tugakerfi.
                  b) Breytið tölunni (FACE)₁₆ í 2-kerfi og tugakerfi.

Takið eftir því að (1)₂ + (1)₂ = (10)₂.   Notfærið ykkur þetta í næsta verkefni.

Verkefni:  a) Leggið saman tölurnar a = (1010)₂ og b = (1111)₂ í 2-kerfi.
                  b) Leggið saman tölurnar a = (32153)₆ og b = (104212)₆ í 6-kerfi.
                  c) Finnið mismuninn b - a í liðum a) og b) í þessu verkefni.

Hér koma tenglar í heimasíður sem að gagni geta komið við verkefnin auk þess sem þar er að finna ítarlegri upplýsingar um talnakerfi:

http://www.danbbs.dk/~erikoest/decimal.htm#top

http://www.brunel.ac.uk/~cs96uub/numsys/decimal.htm

http://www.the-bridge.net/~electrk/appd/number.htm

Bls. 48 - Nemendaverkefni 2

Í ítarefninu er bent á ýmsar fróðlegar vefsíður um gullinsnið og Fibonacci rununa. Notfærið ykkur þær auk neðangreindra tilvísana til að búa til vefsíðu um eitthvert eitt eftirfarandi atriða sem tengjast gullinsniði eða Fibonacci rununni:

a) Stærðfræðingurinn Fibonacci, ævi hans og helstu verk.
b) Gullinsnið í tengslum við byggingarlist, myndlist og tónlist.
c) Ýmsar þrautir og verkefni sem hafa Fibonacci-tölur sem lausn (sbr. vefsíðuna hér):
d) Gullinsnið í náttúrunni (sbr.vefsíðuna hér).
e) Fibonacci runan í náttúrunni (sbr. vefsíðuna hér).
f) Samband gullinsniðs og Fibonacci rununnar, talan Fí, formúla Binet's, Lucas tölur o.fl. 

Bls. 94 - Nemendaverkefni 3

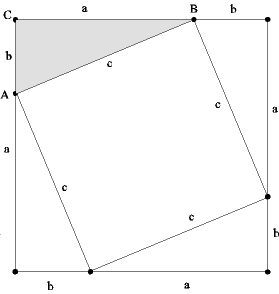
Þetta nemendaverkefni samanstendur af þremur sjálfstæðum verkefnum og í hverju þeirra er regla Pýþagórasar sönnuð.  Í verkefnunum er flatarmál svæðis táknað með því að setja sviga utan um svæðistáknið.  Þannig táknar (ABC) flatarmál þríhyrningsinns ABC.

Verkefni 1: 

Af þríhyrningnum ABC má á eftirfarandi tvo vegu fá ferning með hliðalengdina a + b:

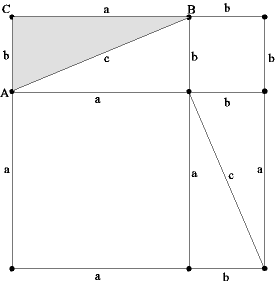
Reiknið flatarmál ferningsins á tvo vegu og leiðið af þeim reikningum reglu Pýþagórasar.

Verkefni 2:

Gefinn er þríhyrningur ABC, a = CB, b = CA og c = AB.  Drögum þrjá ferninga, einn á hverja hlið þríh. ABC, og línu gegnum C hornrétt á AB (sjá mynd):

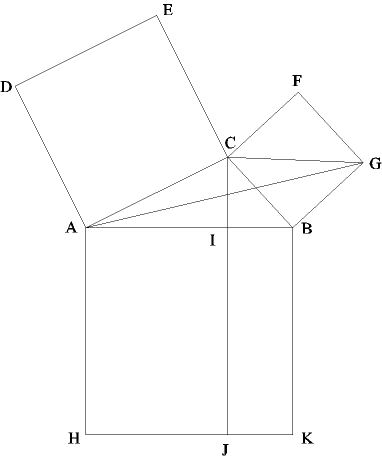
Rökstyðjið eftirfarandi fullyrðingar:
a) (CBG) = (ABG)
    (ABG) = (CBK)
    (CBK) = (IBK)
Af a) leiðir að (CBG) = (IBK) og þar með að (BCFG) = (IBKJ).

Rökstyðjið á sambærilegan hátt og í a) að
b) (ADEC) = (AIJH)

Leiðið af a) og b) reglu Pýþagórasar.

Verkefni 3:

Gefinn er þríhyrningur ABC (C = 90°, a = CB, b = CA og c = AB). 
Fyrst snúum við ABC um 90° um punktinn A.  Fram kemur þá þríh. ADP.
Næst er þríh. ABC fluttur um a í stefnu CB og b í stefnu CA.  Fram kemur þá þríh. DEQ.
BADE er ferningur með c fyrir hlið.  P liggur á DQ, en DQ sker CB í S og SF = a.
Nú eru þríhyrningarnir ABC, ADP, DEQ og BEF eins, en CAPS og SQEF eru ferningar, sá fyrri með hliðinni b, en sá seinni með hliðinni a.

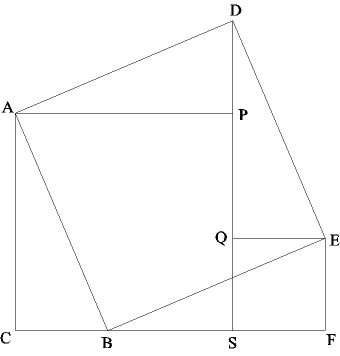
Reiknið nú flatarmál fimmhyrningsins CADEF á tvo vegu og leiðið af því reglu Pýþagórasar.

Bls. 119 - Nemendaverkefni 4

Þetta verkefni samanstendur af fjórum sjálfstæðum verkefnum.  Í því fyrsta á að sýna að liður 1 neðst á bls. 119 sé jafngildur skilgreiningunni á samsíðungi.  Næsta verkefni er að sýna að liður 2 sé jafngildur skilgreiningunni o.s.frv.  Athuga ber, að hér er um tvíleiðingu að ræða í hverju verkefni fyrir sig.

Bls. 138 - Nemendaverkefni 5

Sannið regluna í dæmi 4 í æfingu 5.1I (sem nefnd er Sínusreglan).   Notfærið ykkur í því sambandi reglu 5.15 og það sem fram kemur í dæmi 5.21.
Sannið síðan að nýju Sínusregluna (án tilvísunar til R) fyrir hvasshyrndan þríhyrning án þess að styðjast við ferilhorn.  Ábending:  Dragið hæð á hlið og skoðið rétthyrndu þríhyrningana sem þá koma fram.

Bls. 152 - Nemendaverkefni 6

Upplýsingar um Jörð, sól og tungl í tengslum við dæmi 4:

Radíus jarðar er 6.378·10⁶ m, radíus sólar er 6.9599·10⁸ m og radíus tungls er 1.738·10⁶ m.

Verkefni:  Reiknið sömu hlutföll og í dæmi 4 fyrir allar reikistjörnurnar í réttri röð út frá sólu:
Merkúr, Venus, Jörðin, Mars, Júpiter, Satúrnus, Úranus, Neptúnus og Plútó.
Leitið að heimildum um radíus reikistjarnanna á netinu og getið þeirra.

Verkefni:  Reiknið hlutfallið milli eðlismassa allra reikistjarnanna í réttri röð út frá sólu.  Eins og í fyrra verkefni skuluð þið leita heimilda um massa reikistjarnanna á netinu.

Bls. 178 - Nemendaverkefni 7

Búið til vefsíðu um Ólaf Dan Daníelsson þar sem fram kemur stutt æviágrip hans auk þess sem einn eftirfarandi efnisþátta er tekinn fyrir og athugaður og niðurstöður settar fram á vefsíðunni:

a) Námsferill og starfsævi Ólafs,
b) Kennarinn Ólafur,
c) Skákáhugamaðurinn Ólafur,
d) Vísindamaðurinn Ólafur,
e) Kennslubókin "Reikningbók", útg. 1906,
f) Kennslubókin "Um flatarmyndir - kennslubók í rúmfræði", útg. 1920,
g) Kennslubókin "Kennslubók í hornafræði", útg. 1923,
h) Kennslubókin "Kennslubók í algebru", útg. 1927,
i) Önnur ritstörf Ólafs en að ofan greinir.

Þeir nemendur sem velja einhverja kennslubóka hans skulu skoða hana m.t.t. dæmavals og tíðaranda, bera hana t.d. saman við kennslubækur í stærðfræði í dag o.s.frv.  Gjarnan má taka sýnishorn dæma úr henni og birta á vefsíðunni.
Sem grunnheimild er rétt að nota bók Guðmundar Arnlaugssonar og Sigurðar Helgasonar, sem vísað er til á bls. 178 (Háskólaútgáfan 1996).

Bls. 178 - Nemendaverkefni 8

Búið til vefsíðu um Leif Ásgeirsson þar sem fram kemur stutt æviágrip hans auk þess sem einn eftirfarandi efnisþátta er tekinn fyrir og athugaður og niðurstöður settar fram á vefsíðunni:

a) Námsferill Leifs,
b) Starfsár Leifs á Laugum,
c) Starfsár Leifs við verkfræðideild H.Í.,
d) Vísindamaðurinn Leifur,
e) Helstu verk Leifs.

Sem grunnheimild er rétt að nota bókina Leifur Ásgeirsson, minningarrit, eftir Jón Ragnar Stefánsson (Háskólaútgáfan 1998).

Bls. 185 - Nemendaverkefni 9

Í eftirfarandi verkefnum eigið þið að láta með teikningunni fylgja nákvæma lýsingu í orðum hvernig teikningin var framkvæmd.

1.  Teiknið miðþveril striks.
2.  Teiknið rétt horn.
3.  Teiknið þveril á gefna línu gegnum gefinn punkt.
4.  Helmingið horn.
5.  Teiknð línu gegnum gefinn punkt samsíða gefinni línu.
6.  Skiptið gefnu striki í 3 jafna hluta.
7.  Teiknið þríhyrning úr hlið ásamt hæðinni og miðlínunni á hana.
8.  Teiknið þríhyrning úr tveim hliðum og hæðinni á aðra þeirra.
9.  Margfaldið strik með gefnu hlutfalli.
10. Teiknið þríhyrning úr tveim hornum og ummáli hans.
11. Finnið hlið fernings með sama flatarmál og gefinn rétthyrningur.
12. Teiknið snertil við hring, með gefinni miðju og radíus, sem fer gegnum gefinn punkt utan
      hringsins.

Bls. 189 - Nemendaverkefni 10

1. Í innritanlegum ferhyrningi ABCD er AB = 2, BC = 3, AC = 4 og CD = 1.   Finnið hornin
    ásamt lengd strikanna BD og AD.
2. Í þríhyrningnum ABC eru punktarnir D og E valdir á AB og AC þannig að D liggur á AB og
    AD = AM_b, en E liggur á AC og AE = AM_c.   Sannið að ferhyrningurinn BCED sé innritanlegur.